2D Cartesian Coordinate System
2차원 직각 좌표계.
수평 기준축인 x축과 수직 기준축인 y축이 직각을 이루며 만들어낸 평면 위에 좌표를 기록.
일반적으로 2차원좌표계에서 (x,y)쌍으로 위치를 표현할 수 있고, x,y는 실수범위로 사용가능하지만
그래픽을 전제하는 좌표계에서는 x,y가 정수여야 한다.
(물리적으로 존재하는 Pixel의 위치값이기 때문에 정수일 수밖에 없다)
Scan Conversion?
스캔 변환.
스캔 방식을 이용해 아날로그 도형을 디지털 도형으로 변환하는 알고리즘.
아날로그 도형의 특성등을 스캔하여 어떤 픽셀을 켤지 등의 정보를 비트맵 형식으로 저장함.

예를들어, 아날로그로 표현된 선분을 pixel들의 집합(디지털)로 만들어 냄.

무한한 값으로 표현되는 아날로그와 다르게,
유한개의 픽셀로 표현해야하기 때문에, 아날로그 선분을 완벽하게 재현할 수는 없다.
Basic Line Drawing
선분 그리기.
2차원의 직각좌표계에 두 점을 잇는 직선을 그린다.
이 때 조건
:1. 두 점을 지나는 직선이어야 한다.
:2. 점의 순서는 상관 없어야 한다.(점의 순서가 다르게 주어지더라도 같은 선분을 만들어내야 한다)
:3. 기울기에 무관하게 밝기가 일정해야 한다. (픽셀간의 거리는 좌-우 간 거리보다 대각선 픽셀과의 거리가 루트2배 더 길다)
직선을 그리기 위해 y=mx+b 라는 직선의 방정식을 이용.
두 점(x0,y0) , (x1,y1) 을 방정식에 각각 대입하여 두 개의 방정식을 얻고,
두 식을 연립하여 m과 b의 값을 찾아 사용.
y=m(x-x0)+y0가 됨.
아래는 간단하게 작성한 선분 그리기 코드이다.
int x;
float m,y;
m=(y1-y0)/(x1-x0);
for(x=x0;x<=x1;x++){
y=m*(x-x0)+y0;
setPixel(x,round(y),linecolor);
}과연 조건에 잘 부합할까?
위의 조건 2: 점의 순서는 상관 없어야한다
에서 문제가 발생한다.
x0가 x1보다 값이 큰 경우, 위 코드의 for루프를 돌지 않게 되어 문제가 생긴다.
==> 이를 해결하기 위해, x0>x1인 경우, 두 점의 값들을 swap하여 사용한다.
그런데 또 문제가 있다.
조건 3: 기울기에 무관하게 밝기가 일정해야 한다
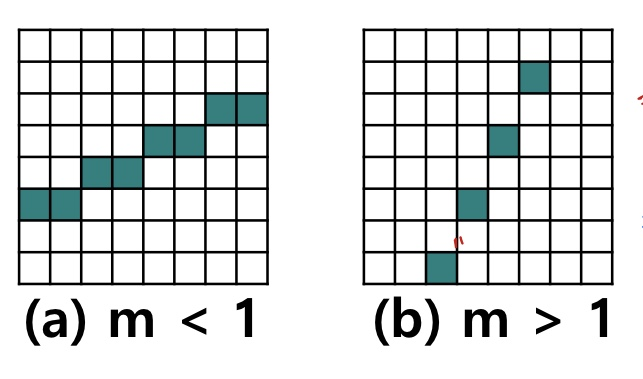
기울기가 1 이상인 경우, 픽셀이 띄엄띄엄 켜지기 때문에 밝기가 감소하게 된다.
왜 이런 현상이 발생했을까?
위 코드에서는 각 x값을 기준으로 y값을 계산해 픽셀을 켜는 동작을 하게된다.
그래서 x좌표의 한 칸에는 픽셀이 단 하나씩만 켜질 수 있었다.
==>이를 해결하기 위해, 기울기가 1 이상인 경우에는 y에 대한 식으로 변경한다.
for(y=y0;y<=y1;y++){
x=((y-y0)/m)+x0;
setPixel(round(x),y,linecolor);
}아마 조건에 따라 이 반복문을 사용하면 될 것 같다.
'2023-1 > 컴퓨터그래픽스' 카테고리의 다른 글
| Parametric Cubic Curves (0) | 2023.06.14 |
|---|---|
| Projections/Curves and Surfaces (0) | 2023.06.14 |
| Viewing 3D world on 2D displays (0) | 2023.05.06 |
| Filling Polygons (0) | 2023.03.20 |
| CG의 HW&SW (0) | 2023.03.08 |

댓글