Single Source All Destinations
하나의 출발점에서 나머지 각각의 vertex들 까지의 최단거리를 구하자..
Dijkstra Algorithm
n개의 vertex가 있다
found[n]배열이 있다.
그래프는 인접 행렬로 표현, cost[n][n]이다.
결과는 distance[n]에 저장한다.
#define MAX_VERTICES 6
int cost[][MAX_VERTICES] =
{ {0,50,10,1000,45,1000},
{1000,0,15,1000,10,1000},
{20,1000,0,15,1000,1000},
{1000,20,1000,0,35,1000},
{1000,1000,30,1000,0,1000},
{1000,1000,1000,3,1000,0} };
int distance[MAX_VERTICES]; //결과를 저장할 배열
int n = MAX_VERTICES;
short int found[MAX_VERTICES];
int choose(int distance[], int n, short int found[]) {
int i, min, minpos;
min = 1e9;
minpos = -1;
for (i = 0; i < n; i++) {
if (distance[i] < min && found[i] == false) {
min = distance[i];
minpos = i;
}
}
return minpos;
}
void shortestpath(int v, int cost[][MAX_VERTICES], int distance[], int n, short int found[])
{
int i, u, w;
for (i = 0; i < n; i++) {
found[i] = false;
distance[i] = cost[v][i];//v에서i로 가는 길
}
found[v] = true;
distance[v] = 0;//현재노드
for (i = 0; i < n - 2; i++) {
u = choose(distance, n, found); //choose는 선택하지 않은 노드 중 최단거리가 가장 짧은 노드를 선택
found[u] = true;
for (w = 0; w < n; w++) {
if (found[w] == false)
if (distance[u] + cost[u][w] < distance[w])
distance[w] = distance[u] + cost[u][w];
}
}
}
1) (참고: 이해가 쉽도록 하기 위해 1번vertex의 정보는 distance[1], found[1]에 저장한다고 하자)
vertex 3에서 시작한다고 하자.
distance[]는 3에서 각각의 vertex로 가는 비용을 그대로 적어준다. (표에서 1000은 무한을 표현한 것임)
found[]는 false로 초기화하고, 자기자신만 found[3]=true로 변경한다.

2)
found가 false인 것 중에서 distance가 가장 작은 것을 선택한다.(코드에서는 choose함수)
distance[4]=15, found[4]=false 인 4번 vertex가 선택되었다.
found[4]=true로 변경하고,
found==false인 것들 중 4번vertex를 거쳐 가는것이 더 가까운것을 찾아 바꿔준다
여기서는 2번,5번이 변경되었다.
2번은 원래 거리가 무한대였지만, 4번을 거쳐 가게되면 distance[4] + cost[4][2] = 30으로 더 작아졌다.
5번도 원래 거리가 무한대였지만 4번을 거쳐 가게 되면 distance[4]+ cost[4][5] = 50으로 더 작아졌다.

3) 이후 2번과정을 똑같이 반복한다.
이번에는 1번vertex가 선택되었군.
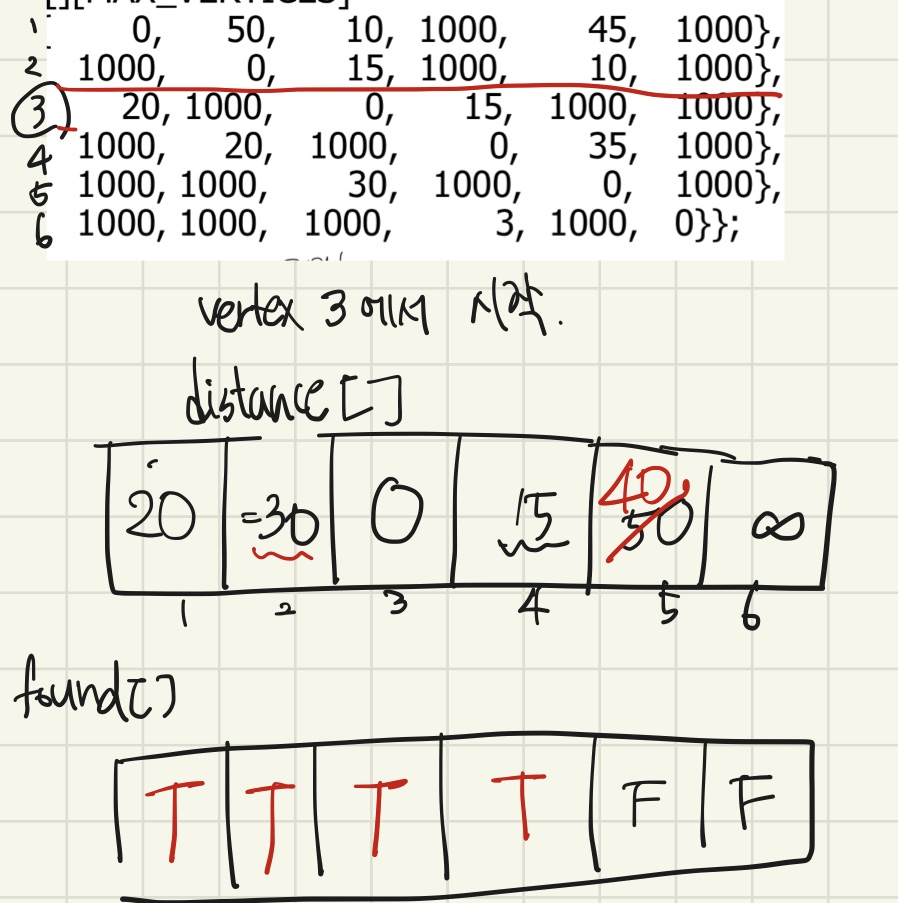
2번vertex 선택

5번 vertex 선택.
이제 하나의 vertex만 제외하고 모두 선택되었는데,
사실 마지막 vertex는 꺼내볼 필요가 없다. (다른애들이 이미 최단거리를 찾았음..)
그래서 반복문도 n-1번만 도는 것.
시간복잡도는 O(n^2)이다.
All Pairs Shortest Paths
모든 점에서 모든 점까지의 최단 경로를 찾기.
다익스트라 알고리즘을 n번 돌려도 될것같긴 하나, 복잡도가... 좀 더럽긴 하다.
동적 프로그래밍 방법을 이용한 풀이를 보자.
void allcosts(int cost[][MAX_VERTICES], int distance[][MAX_VERTICES], int n)
{
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
distance[i][j] = cost[i][j];
}
}
for (int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (distance[i][k] + distance[k][j] < distance[i][j])
distance[i][j] = distance[i][k] + distance[k][i];
}
}
}
}또잉?
코드는 오히려 더 쉬워졌다.
...
반복문 안의 if문을 보자.
......이렇게 생각하면 쉬울 것 같다.
i에서 j로 가는 최단거리는 distance[i][j]에 저장되어있다.
근데 k를 거쳐서 가는게 더 짧을수도 있지 않나?
k를 거쳐가는 distance[i][k]+distnace[k][j], 기존의 최단거리 distance[i][j]를 비교하고,
더 작은값을 distance[i][j]에 저장하자.
이행적 폐쇄(Transitive Closure)
이 vertex에서 저 vertex까지 갈수있는 경로가 존재하나? 를 담은..배열이라고 보면 될것같다.
위의 allcosts()알고리즘에서, if문이 있는 부분을
distance[i][j]=distance[i][j] || distance[i][k] && distance[k][j]
로 바꿔주면 된다.

'2022-2 > 자료구조' 카테고리의 다른 글
| [자료구조] 7. Sorting (0) | 2022.12.03 |
|---|---|
| [자료구조] 그래프 - 작업 네트워크 (1) | 2022.11.29 |
| Biconnected Components/최소 비용 신장트리 (0) | 2022.11.22 |
| 6장 - 기초적인 그래프 연산들 (1) | 2022.11.18 |
| 6. Graphs (0) | 2022.11.14 |



댓글